Mathematical libraries are a key component of the software stack for exascale-class applications. As a matter of fact, exascale computing deployment is conditioned by the development of new suitable numerical algorithms, since most of existing ones are not able to face many issues raising into the race to exascale.
Mathematical libraries provide building-blocks implementing up-to-date methods and algorithms that application developers can reuse in form of highly-reliable and high-performance components.
Any new generation of computer architectures brings new challenges to achieve high performance mathematical solvers and a bi-directional interaction between new computer architectures/environments and new mathematical software is ever more crucial for deployment and effective use of the new technology to advance in Science, Industry and Society.
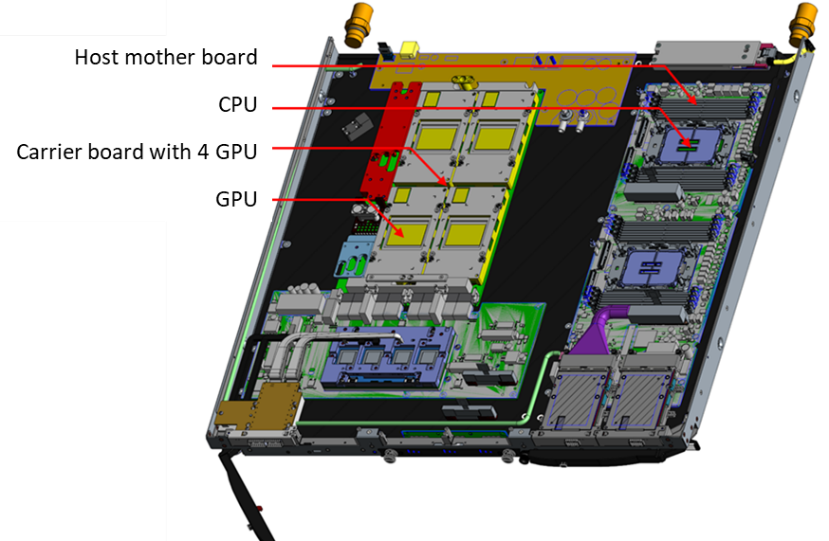
The need to improve computing performance in the near and medium term indicates that exascale and also post-exascale platforms will continue to emphasize heterogeneity. This type of architecture exploits at node level, accelerators such as modern GPUs and reconfigurable hardware such as FPGA to boost performance and also energy efficiency in computations. As computer architectures become heterogeneous, there is the need for algorithms that support mixed-precision and minimize communications among the different devices and memory levels. The new power-to-solution metrics requires a rethinking of many computational kernels of HPC applications looking for the best trade-off between the reduction of the energy consumption and the minimization of the time-to-solution, promoting reproducibility and scalability.
We will provide new high-performance algorithms and software modules for some of the so-called Colella’s dwarves, who identified numerical methods crucial for science and engineering. In particular, we will focus on algorithms and software for sparse linear algebra, where data sets include many zero-values and are usually stored in compressed data structures to reduce storage and memory bandwidth requirements,hey are generally accessed with indexed loads and stores, and main computational kernels are communication bound.
The library kernels will be of immediate use in a wide range of applications, ranging from classical scientific simulation to AI techniques, including automatic pattern recognition in complex systems, and will be tested in some of the applications proposed as use cases in this project.
Leading Partner: CNR


About the author